摘要：最近，借着生日的契机，在公众号里进行了一次「撒币」游戏。让我们回顾一下这次游戏里有哪些有趣的事情吧。

最近，借着生日的契机，在我的公众号里进行了一次「撒币」游戏。原本是在微观经济学课上玩过一个类似的游戏，突然奇想就亲自组织了一次。让我们回顾一下这次游戏里有哪些有趣的事情吧。

01. 游戏规则

本次撒币游戏的规则如下：在本号后台回复1-100的一个整数即可参与，活动结束后，回复没有与其他人重复的最大数字的同学即为本次的赢家，可以获得价格等于该数字的红包或礼物。

从规则中可以看出玩家的报酬情况是，获胜玩家的报酬等于其选择的数字，其余玩家报酬为0。当然，存在一种特殊情况是，如果所有数字均有重复，则无人获得奖金，庄家是唯一赢家。为了分析方便，我们认为此时所有人的报酬是负数，即所有人都会厌恶从而避免这种情况。

02. 条件分析

从游戏的规则设定中，我们可以知道什么呢？

• 虽然所有人做出决策的时刻不同，但由于截止时间前每个人的决策结果对其他人是不可见的，所以游戏的过程可以视为一次静态博弈。
• 每个人的预期报酬是由自己所选的数字决定的，报酬的定价机制会激励玩家选更大的数字。
• 结合游戏规则可以看出，越少的玩家参与，每个玩家获胜的几率都会越高，没有激励会使得玩家转发这次游戏，所以这次游戏是几乎没有二次传播性的（忧伤）。
• 果然，从推送的阅读量可以估计出游戏的参与人数基本是100以内（忧伤x2），可以断定绝大多数玩家都是庄家TT的一度联系人，由此可以推出玩家群体中应该存在多个互相熟悉的社交圈。再考虑到奖金的可分性，于是存在合作的可能性。
• 由于规则没有禁止玩家间的交流，每名玩家可以通过线上或线下的渠道发表任意的观点，玩家间的交流是可能的。

03. 策略设计

一、不合作下的情况

首先定义一下纳什均衡（Nash Equilibrium）的概念。对于一个博弈问题，如果固定其他所有人的策略，任一参与者不能通过改变自身的策略获得更好的报酬，就达到了一个纳什均衡。通俗地说就是，谁先动谁就输了。具体可以参见维基或百度。

如果从“理性人”的假设出发，显然所有玩家决策的策略应该是一样的。如果每名玩家的策略是选择一个确定的数字，则所有玩家都会选择一样的数字，此时任意一名玩家选择另外一个数字，TA就成为了唯一的赢家（假设玩家数≥3），所以容易推出确定策略的均衡是不存在的（即不存在纯策略纳什均衡）。于是考虑混合策略。混合策略的决策是定义在策略集上的一个概率分布，比如以50%概率选100，50%概率选99。

由于玩家数量不确定，我们按照玩家数量从少到多逐步分析。

• 如果只有2名玩家，容易知道在没有合作的情况下，每人的最优方案都是选100，是存在纯策略纳什均衡的。当玩家数≥3后，如上所述，纯策略的均衡就不存在了。
• 如果有3名玩家，情况复杂一些。尝试证明了一下，混合策略下的纳什均衡解是分布在1-100上的一个概率分布，每一个数字都有可能被选中，并且选择更大的数字概率更高（过程见附录）。
• 于是显然，当玩家数更多的时候，混合策略下的纳什均衡解同样也是1-100上的一个概率分布，选择大数的概率更高。

不合作的情况下，能分析的内容到这里似乎就结束了。我猜多数人看到这里的想法是：这有什么用？（当然我没法验证这个想法。）这就反映了推理本身的出发点「理性人」的假设是不对的，在现实中，除了学习或者研究外，几乎没有人是具有能力并且愿意进行无限推理的。理性是有限的，才是更现实的情况。

二、允许合作下的情况

考虑如下的情况，有一名玩家A通过某种渠道告知游戏中其他所有玩家：我选了100。这时其他所有玩家会怎么做呢？如果选择100，自己就和A一起输掉了，这时候其他玩家就有机会获胜了；而如果所有人都不选择100，则A如果真的选择了100，就获胜了。那么是否会有人选择100呢？如果假设所有人是理性且自私的，在没有合作的情况下，是不会有人选择100的。

为了不让A获胜，该怎么办呢？于是合作和联盟出现了。B和C是室友，在商议之后决定，B选择100，C选择99，如果C获奖的话，BC平分奖金。通过这种策略，BC的联盟成功击败了A这种看似必胜的策略，并且任一单独的玩家是不可能战胜BC的联盟的。合作博弈下，联盟通过降低联盟外玩家的胜率，提高了自己内部的胜率。那么如果战胜BC的联盟呢？更大的联盟。DEF三人的联盟选择了98，99和100，BC联盟就失败了。

推广下去，更大的联盟就意味着更高的赢面。当玩家数不超过100时，必胜的方案是组织起一半的玩家，从大到小依次选择100, 99, 98…这时联盟外的玩家是不可能获胜的，联盟平分了奖金。当然，游戏的奖金金额能否激励大家去组织这样的事情，就是另外一个问题了，唉，穷。

04. 结果统计

最终有50名有效的玩家参与了这次游戏，其中数据的茎叶图如下。最终获胜的是选择98数字的同学。

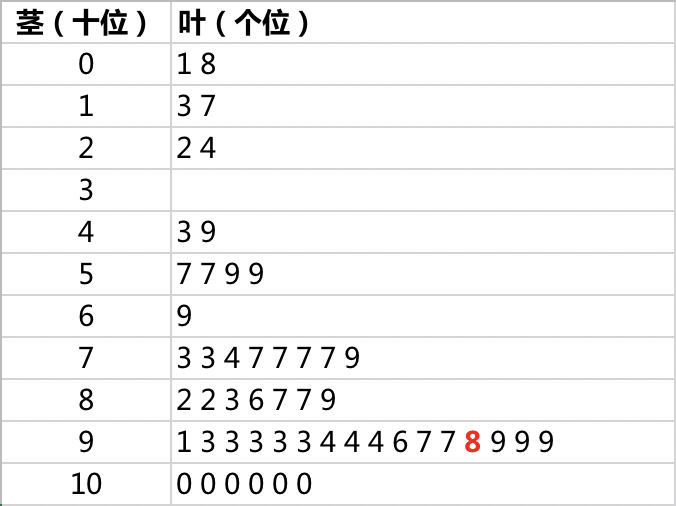
05. 结果分析

从最后的数据中，我们可以看到些什么呢？

• 有8名玩家选择了50以下的数字。由于奖励是与选择的数字挂钩的，无论从何种角度来看，这都不像理性人所作出的决策。为什么会出现这批玩家呢？我猜测是这样的金额不足以引起他们的兴趣，皮这一下的快乐远胜过金钱，所以…欢迎土豪们！
• 有20名玩家选择了50-89。由于没有实际采访过这些玩家，所以无法断定他们的动机。我的猜测是他们对整个游戏的玩家规模有着错误，具体来说是，过于乐观的估计，所以保守选择了偏小的数字，尤其是70-89的玩家。
• 剩下的22名玩家分布在91-100的区间内。这部分竞争颇为激烈，根据我在后台的观察，如果按照时间顺序列出获奖数字的话，是94-99-100-96-97-98，胜与负就在一念之间，激进的人群里偏保守的玩家笑到了最后。
• 除了分布，这个结果还能给我们什么样的启发呢？如果想赢的话，别选特殊数字。77（嗯很多人的幸运数字）、93、94（出生年份）、97（100内最大的质数）上发生了大量的撞车，就是最好的体现。当然，有些玩家是执意选择幸运数字的，这就是另一回事了。

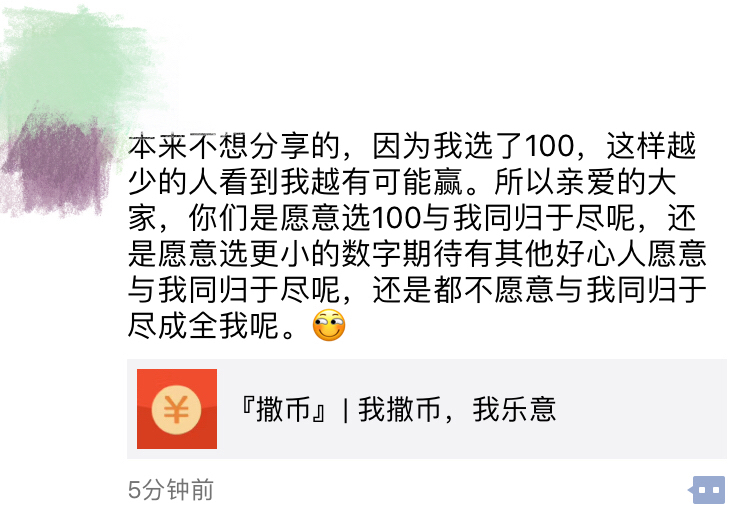
除了结果外，游戏的过程中也发生了一些有趣的事情。在条件分析和策略设计里，我们提到，玩家间的交流是可能。在实际游戏过程中，真的出现了这样一位「戏精」同学，简直是读着剧本进行的演出：

• 在自己的朋友圈内尽可能广播自己选择100的消息，
• 向其他人强调了选择100的同归于尽的后果，
• 以及，“本来不想分享的”充分证明了本次活动没有二次传播性（心累）。

在知道TA最后选了啥之后…我决定颁发一枚「最佳戏精奖」👏

这次的分析就到这里了。如果你有关于这次活动有什么想法，或者有什么新活动的点子，欢迎关注我的公众号跟我交流呀。

参考资料

• 知乎 | 10个人各自从1-10选数字，尽量让自己最大且不重复，如何选？

附录

三名玩家进行游戏的纳什均衡分析

按照每个人的策略集中的选项数进行分类讨论。显然选项数应该大于1。

1. 如果包含两种选项，则一定是100和99，假定最优的混合策略为以概率$p$选100，概率$1-p$选99。
   • 首先求解均衡策略。均衡时，选择100和99的预期报酬应该是一样的（即混合策略纳什均衡成立的条件），否则玩家一定会选择预期报酬更高的数字，混合策略就失效了。选择100的预期收益为$100(1-p)^2$，选择99的预期收益为$99p^2$，令它们相等。由于$100 \approx 99$，可以约掉，于是解出$p=0.5$，即50%概率选100，50%概率选99。如果所有人都选择该策略，则每个人获胜的概率为1/4，预期报酬为25。
   • 下面需要验证一下，该策略是否是最优的。固定前两名玩家使用该策略，我们从第三名玩家的角度验证一下该策略是否可以改进。可以发现，如果三个人都选择一样的数字（概率为1/4），则没有人获胜，是否可以利用这种情况来提高自己的胜率呢？答案是可以的。例如，第三名玩家可以采用这样的混合策略：50%的概率选择100，各25%的概率选择99和98。稍加计算可以得出TA的获胜概率约5/16（认为$100 \approx 99 \approx 98$），大于1/4，则该策略不是纳什均衡的。
   • 所以，不存在包含两种选项的均衡混合策略。
2. 如果包含三种选项，则一定是100，99和98。用类似的方式求解，依然可以发现该策略也不是最优的，存在包含四种选项的解可以严格更优。
3. 于是猜想均衡时的混合策略，在1-100中所有数字上都应该有概率选中。采用反证法证明。如果两名玩家只选中部分数字，则第三名玩家可以通过利用前两人选中一样数字的情况来提高自己的胜率。此猜想可以证明如下：